Some other gas laws

 Combained law

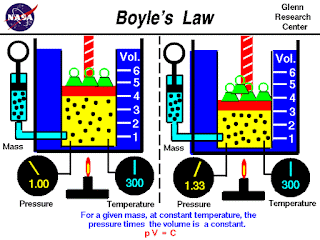
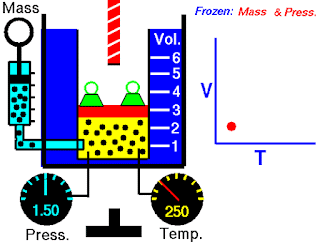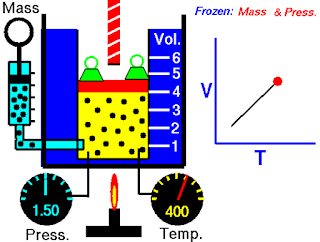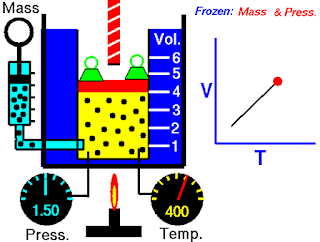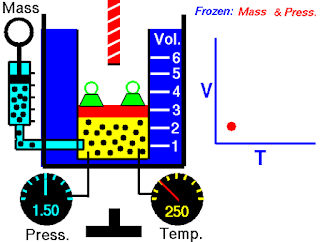
As all gases behave the same way with respect to pressure, volume, and temperature, if the amount is measured per mole, then the ideal gas expression itself can be written as a ratio useful in the events like when temperature, volume, and pressure of a fixed amount of gas vary from (T1, V1, P1 ) to (T2, V2, P2). For such an instance we can write,for the initial condition; 𝑛𝑅 =𝑃1𝑉1/𝑇1

for the final condition; 𝑛𝑅 =𝑃2𝑉2/𝑇2

               𝑃1𝑉1/𝑇1=𝑃2𝑉2/𝑇2

Dalton law of partial pressure 

In most practical applications we encounter a mixture of gases rather than a single gas. The air we breathe has nitrogen and oxygen gases as major components and a variety of other gases in minute quantities. All of these gases contribute to the total atmospheric pressure. 

Also, the pressure that a constituent gas of a mixture of gases would exert if it alone occupies the volume of the mixture at same temperature is defined as the partial pressureof that gas. A postulate introduced by Dalton says that the total pressure exerted by the mixture of non-reactive gases is equal to the sum of the partial pressures of individualgases. This is known as “Dalton law of partial pressures”. Accordingly, if partial pressures of individual gases in a mixture of gases A, B and C are PA, PB and PC respectively, at constant temperature and constant volume the total pressurePT of the mixture is given by the following equation.

             PT = PA + PB + PC

The Dalton law of partial pressure can be derived using ideal gas equation as follows. Consider a mixture of gases A and B with nA and nB moles, respectively exerting the total pressure of PT.

                      PV = nRT

For gas A, nA = PAV/ RT (PA is the partial pressure of gas A)

For gas B, nB= PBV/ RT (PB is the partial pressure of gas B)

For the mixture of gases, nT = PTV/ RTand nT = nA + nB

Therefore, PTV/ RT = (PAV/ RT) + (PBV/ RT)

Simplification gives , PT = PA + PB

This is the Dalton law of partial pressures.

Suppose at the temperature T, nA moles of gas A and nB moles of gas B, are enclosed in acontainer of volume V, then partial pressures exerted by gases A and B are PA and PBrespectively while the total pressure is PT. 

Therefore, we can write, 𝑃𝐴 =𝑛𝐴 𝑅𝑇/𝑉

and 𝑃𝐵 =𝑛𝐵 𝑅𝑇/𝑉

According to Dalton law, 𝑃𝑇 = 𝑃𝐴 + 𝑃𝐵

Substituting from the above, 𝑃𝑇 =𝑛𝐴𝑅𝑇/𝑉+𝑛𝐵 𝑅𝑇/𝑉

= ( 𝑛𝐴 + 𝑛𝐵)𝑅𝑇/𝑉

Dividing the expressions for 𝑃𝐴 and 𝑃𝐵 separately by 𝑃𝑇, we get;

𝑃𝐴/P𝑇=[𝑛𝐴 𝑅𝑇/𝑉]/( 𝑛𝐴 + 𝑛𝐵) 𝑅𝑇/𝑉

=𝑛𝐴/( 𝑛𝐴 + 𝑛𝐵)= 𝑥𝐴 this is the mole fraction of A

Likewise, 

𝑃𝐵/𝑃𝑇=[𝑛𝐵 𝑅𝑇/𝑉]/( 𝑛𝐴 + 𝑛𝐵) 𝑅𝑇/𝑉

=𝑛𝐵/( 𝑛𝐴 + 𝑛𝐵)= 𝑥𝐵 : this is the mole fraction of B

Therefore, we can write,

         𝑃𝐴 = 𝑥𝐴 𝑃𝑇 and 𝑃𝐵 = 𝑥𝐵 𝑃𝑇

Partial pressure of the constituent gas is equal to the product of total pressure and mole fraction of the gas.

We apply our knowledge on Dalton law for a mixture of gases assuming that they have the same properties as pure gases, provided that all gases in the mixture are ideal gases thus do not react chemically with each other. However, in practical situations such as chemical reactions involving gases, the procedure used to collect may introduce another gas. For example, a technique often used to collect gases from a chemical reaction is the displacement of water from an inverted container. In this method, a gas is collected in the container by bubbling the gas through a tube into a gas jar filled with water which is placed upside-down in a water trough. So that the gas push all the liquid out from the bottle when it is collected. Here, we assume that the gas does not dissolve in water and does not react with water. However; we do not get the gas which is in the pure state. Instead, the collected gas is a mixture of the gas generated by the reaction and some water vapour formed from evaporation. The amount of water vapour contained in the gas is most readily measured by the pressure it exerts at that temperature, called the saturated vapour pressure. Therefore, to determine the pressure exerted by a gas collected in thisway at a specific temperature, it is necessary to subtract the vapour pressure of water from the total pressure of the mixture. Then from the partial pressure of the gas and its volume and temperature, the ideal gas law can be used to calculate the amount of the gas collected. 

This video is taken from youtube from the channel 

This page is create with the help pf resource book of physical chemistry.@www.nie.lk 

SIMPLE GAS LAWS

 Introduction 

The gas laws that we are going to discuss are the results of experiments carried out by several scientists on the physical properties of gases. In these experiments, relations among the variables of pressure, temperature, volume and amount of gases are considered and the results provide valuable information on the gaseous state of matter in turn helping the mankind in many ways.

Ideal gas and Ideal gas equation

When it is assumed that intermolecular forces do not exist among the molecules of a gas,such a gas is called an ideal gas. That is molecules in an ideal gas do not exhibit attraction or repulsion among them. Furthermore, the volume of ideal gas particles is considered negligible when compared to the volume of the container.The absolute temperature (T), pressure (P), volume (V) and the amount (n, moles) of a gas are the factors that affect the behaviour of a gas. P, T, V and n are related by the expression

                       𝑷𝑽 = 𝒏𝑹𝑻

The value of the constant R for one mole of an ideal gas can be calculated under theconditions of 0 °C and 1 atm as given below: (At 0 °C and 1 atm, the volume of one mole of ideal gas is 22.414 dm3)

𝑅 =𝑃 𝑉/𝑛 𝑇

=101325 Pa × 22.414 × 10−3 m3/1 mol × 273.15 K

= 8.314 J K−1 mol−1

We can see that the ideal gas equation is a relationship among four variables and it describes the state of any gas. Therefore, it is also called equation of state.

The ideal gas law allows us to determine any one of the quantities volume, pressure, temperature, or moles of the gas when the other three are given. If the amount of moles of the gas is known, we can also calculate its mass using its molar mass. Further it can also be used to determine the density of a gas. It is important to keep in mind that all the other quantities must be in units that match the value used for the ideal gas constant. Usually pressure can be expressed in several units such as atm, Pa, bar, torr, etc.

 There are insights into the ideal gas equation that it can be expressed in different forms to estimate mass and density of a given gas with simple modifications as shown below. 

PV = n RT and we can write,

               P = (𝑛/𝑉)𝑅𝑇

                    𝑷 = 𝑪𝑹𝑻, 

where C is the concentration

We can also write PV = nRT as

               PV = (𝒎/𝑴)𝑹𝑻 ,

where, m is the mass and M is the molar mass of the gas.

Also we can write the above as;

               P = (1/M)(𝑚/𝑣) 𝑅𝑇

                   P = 𝒅 𝑹𝑻/𝑴

where, d is the density and 𝑑 =𝑚/𝑣

1.Boyle law👇

That is the “pressure of a fixed amount (mass) of gas at constant temperature inverselyvaries with (or proportional to) the volume of the gas”. This is known as the Boyle Law(1627-1691) which was named after Robert Boyle, an Irish scientist in the seventeenth century who studied change in volume of a gas when pressure of a gas is varied under constant temperature conditions. Mathematical form of it, is given below.

                     𝑃 ∝1/𝑉

            𝑜𝑟 𝑃 =𝑘/𝑉; k is a constant

The ideal gas law can be used to derive Boyle law as follows.

                         PV = nRT

If the amount of the gas and temperature of the system are kept constant, then the product nT is a constant. Since R is also a constant, then the product, nRT = k (a constant)

                        PV= k

It means that “at constant temperature, the product of pressure and volume of a fixed amount of gas is constant”. This is another way of expressing Boyle law.If a fixed amount of gas at constant temperature T occupying volume V1 at pressure P1undergoes change, so that volume becomes V2 and pressure becomes P2, then according to Boyle law             

                    P1V1 = P2V2

2.Charles law 

Investigations by the scientists Jacques Charles and Joseph Gay-Lussac have showed that for a fixed amount (mass) of a gas at constant pressure volume of a gas increases on heating and decreases on cooling. It was also found that for each degree change (rise or fall) in temperature, volume of a gas changes (increases or decreases) by a factor of 1/273.15 of the original volume of the gas at 0 C.Assume that volumes of the gas at 0 °C and at t °C are V0 and Vt respectively, then we can write,

𝑉𝑡 = 𝑉0 + (𝑡/273.15)𝑉0 = 𝑉0 (1 +𝑡/273.15) = 𝑉0 (273.15 + 𝑡/273.15 )

At this stage, a new scale of temperature is defined such that t °C on new scale is given by

              Tt = 273.15 + t

and 0 °C will be given by T0 = 273.15

This new temperature scale is called the Kelvin temperature scale (K) or absolute temperature scale. -273.15 °C (0 K) is also defined as the thermodynamic zero, which is the lowest theoretically reachable temperature.

By applying this temperature scale, we can rewrite the relation 

       𝑉𝑡 = 𝑉0 (273.15 + 𝑡/273.15 ) as, 

                     𝑉𝑡 = 𝑉0 (𝑇𝑡/𝑇0) 

Hence, 

                       𝑉𝑡/𝑉0=𝑇𝑡/𝑇0

For a general case when the change occurs from (V1, T1) to (V2, T2) at constant pressure

                       𝑉1/𝑉2=𝑇1/𝑇2

This can be rearranged as 

                𝑉1/𝑇1=𝑉2/𝑇2

𝑉/𝑇= constant or 𝑉 = 𝑘 𝑇

Therefore, “the volume of a fixed amount of gas under constant pressure is directly proportional to the absolute temperature of the gas.” This is called Charles law.

Further, the ideal gas law can be used to study the effect of temperature on the volume of a gas if the pressure of the system is kept constant for a fixed amount of a gas. The ideal gas law can be rearranged as follows;

                       PV = nRT

                       V = nRT/ P

When the pressure of a fixed mass of gas is constant, 𝑛𝑅/𝑃is constant.

                V ∝ T or 𝑽 = 𝒌𝑻

Let’s consider the equation 𝑉𝑡 = 𝑉0 (273.15+ 𝑡/273.15 ) and substitute t = -273.15, where we get the volume of the gas equal to zero meaning that the gas will not exist. Therefore, we can understand that all the gases get liquefied before this temperature is reached. The lowest hypothetical or imaginary temperature at which gases are supposed to occupy zero volume is called absolute zero.

3.Avagardo law

Upon the developments of Boyle and Charles laws, in 1811 Italian scientist Amedeo Avogadro tried to combine conclusions of those with the amount and volume of a gas andpostulated a new hypothesis which is now known as Avogadro law. It states that equalvolumes of all gases under the same conditions of temperature and pressure contain equal number of moles (Avogadro Law).

                      i.e. V ∝ n

        or we can write V = k n

The number of molecules in one mole of a gas has been determined to be 6.022 * 10^23and also known as Avogadro constant (denoted as NA or L).

Avogadro law can be easily understood with the help of the ideal gas law as follows.

                        𝑃𝑉 = 𝑛𝑅𝑇

                       𝑉 =(𝑅𝑇/𝑃)× 𝑛

         𝑉 =(𝑅𝑇/𝑃)×(𝑁/𝑁𝐴)=𝑅𝑇/𝑃𝑁𝐴× 𝑁

Here, N and NA are the number of molecules of the gas and the Avogadro constantrespectively. By applying the above relationships to equal volumes of gases P and Q at the same temperature and pressure,

                   𝑉𝑃 =𝑅𝑇/𝑃𝑁𝐴× 𝑁𝑃

                  𝑉𝑄 =𝑅𝑇/𝑃𝑁𝐴× 𝑁𝑄

At constant P and T, we can write (as R and NA are constants)Simply it says that for a gas at constant temperature and pressure equal volumes of gases have equal number of molecules. i.e. V∝N

It is useful to understand that the gas laws discussed above can also be used to obtainthe ideal gas equation for a given volume V of a gas. 

Boyel Law ∶ 𝑉 ∝1/𝑃− − − − − (1)

Charles Law ∶ 𝑉 ∝ 𝑇 − − − − − (2)

Avogardro Law ∶ 𝑉 ∝ 𝑛 − − − − − (3)

The only equation that fulfills (1), (2) and (3) is,

                   𝑉 ∝(𝑛/T)𝑃

                    𝑃𝑉/𝑛 𝑇= 𝑘

                   When 𝑘 = 𝑅

                      𝑃𝑉 = 𝑛𝑅𝑇

This video is taken from youtube from the channel of crash course

    To be continued.............

Made with the reference of chemistry resource book physical chemistry part -1 @www.nie.lk

      

GASEOUS STATE OF MATTERS

 Introduction 

Everything in the universe has a chemical identity. We know that the smallest particle of matter is an atom. “Study of matter and the changes that it undergoes” can simply be understood as the basic definition of chemistry. Usually matter is anything that occupies space and has mass and can be seen and touched (such as soil, water) as well as things we cannot see such as air. Based on the composition and properties, several categories such as substances, mixtures, elements as well as atoms and molecules can be identified. All substances, at least in principle, can exist in three states: solid, liquid and gas. In a solid, particles are held tightly and close together in an ordered structure with a definite shape having a small degree of motion. Particles in a liquid are close together but are not held so tightly in position and can move faster compared to that of solid. Gases differ largely from liquids and solids in the distances between the particles. In a gas, the particles are separated by distances, large compared with the size of the particles allowing them to behave freely. Therefore, the attractive forces between gas particles are very small or negligible and that allows us to consider gas particles individually and some hypotheses are easily predictable depending on the temperature and pressure changes.

Behaviour of particles and their characteristics in solids ,liquid and gases.

Anything that occupies space and has a mass can be called “matter”. This could be things we can see and touch like trees or things we cannot see like the air we breathe. All matter can be classified broadly into three states solid, liquid and gas. Matter can be interconverted among these three states without changing the composition. For an example water in liquid state can be converted to gaseous state (steam) when heated and can be converted to a solid (ice) if cooled.

Three states of matter differ based on arrangement and movement of particles. The inter-particle distance is highest in gaseous state and lowest in solids. In liquid state, particles are relatively closer compared to gaseous state, yet not too close compared to the solid state. Therefore, a regular pattern of particles can be seen only in solid state, while both gaseous and liquid state particles show random arrangement. As a result, particles in gaseous state can move fast and freely compared to liquid state particles. However, movement of particles in solids is limited to vibrations. The arrangement and motions of particles in matter result in differences in macroscopic properties such as volume, shape, compressibility and density as indicated in the Table below👇

Note: Here we say that a liquid takes the shape of the container and we have to thinkwhy we get these shapes. Usually, particles of any object is being pulled by a variety of forces such as intermolecular forces, and that’s why it has shape. Some given amount (volume) of water in a beaker is being shaped by surface tension resulting from intermolecular forces within the liquid creating a meniscus curve at the edge of the surface, by the force of the walls of the beaker pushing up on it, and by the gravity which is greater than the surface tension, pulling it down. So, it takes the shape of the beaker, with a flat surface on the top. This happens due to the satisfaction of all those different forces. However, in the case that the surface tension is stronger than gravity, the water’s surface might not lie flat by taking the shape of the container. Assume that there is no gravity, and so surface tension is very much high. As each part of the surface wants to stay as close as possible to the rest of the surface it tries to minimize the forces within. So,the shape that best allows this is a sphere, because it is the shape that has the minimal surface area for a given volume.

Matter in one particular state can be converted to another state by heating or cooling. Increase of temperature makes particles move faster and inter-particle distance becomes greater leading to change in state. Accordingly, increase in temperature converts solid state materials to liquid and liquid state materials to gaseous state. The opposite happens with decreasing temperature. Figure illustrates how matter can be interconverted among states.

As an example for above process.Let, take water as example ,

When we describe the properties of the three states of matter with the help of Table(see the comparisontable),motion and arrangement of particles are basically considered. Especially, thermal energy is the energy of a body arising from motion of its atoms or molecules and it is directly proportional to the temperature of the substance. Therefore, it measures the average kinetic energy of the particles of the matter and is thus responsible for movement of particles or the thermal motion.

As we already know, interparticle forces tend to keep the particles together but thermal energy of the particles tends to keep them apart. Therefore the existence of three states of matter can be regarded as a result of balance between interparticle forces and the thermal energy of the particles.When inter molecular interactions are very weak, molecules do not tend to make liquid or solid unless thermal energy is reduced by lowering the temperature. Gases do not liquefy on compression only, although molecules come very close to each other andintermolecular forces operate to the maximum. However, when thermal energy of molecules is reduced by lowering the temperature, the gases can very easily be liquefied.These behaviours can be explained by Figure (see the above figure)where we can understand the reversible nature of intermolecular forces and the thermal energy acting on the three states of matter.

GASEOUS STATE OF MATTERS 

Let us now focus our attention on the behaviour of substances which exist in the gaseous state under normal conditions of temperature and pressure. 

The gaseous state is characterized by the following physical properties as described in Table above.

👊 Gases are highly compressible.

👊 Gases exert pressure equally in all directions.

👊 Gases have much lower density than the solids and liquids.

👊The volume and the shape of gases are not fixed. These assume volume and shape of the container.

👊Gases mix evenly and completely in all proportions without any mechanical aid.

Simplicity of gas is due to the fact that the forces between their molecules are negligible.Their behaviour is governed by same general laws (will be discussed later), which were discovered as a result of experimental studies. These laws are usually relationships between measurable properties of gases. Some of these properties like pressure, volume, temperature and amount (moles or mass) are very important because relationships between these variables describe state of the gas.

Interdependence of these variables leads to the formulation of gas laws.

Made With reference of 

Chemistry Resource Book - Physical Chemistry -Part I

LEWIS diagrams

 Lewis dot diagram and lewis dot-dash diagram

 Lewis dot diagram is used to illustrate the atomic skeleton, nature of the bonding present (single, double and triple bond) and the distribution of the valance shell electronsaround each atom of the given chemical formula. In Lewis dot-dash structure, a bonding electron pair is denoted by a short line drawn between the two atoms.

👉Chemical formula =Cl2 

👉Lewis dot diagram 

👉Lewis dot-dash structure

👊The following factors need to be considered when drawing Lewis dot diagrams:

🤜 Elements H and F are generally not considered as the central atom since these can form only single bonds. Atoms which are capable of forming multiple bonds are  placed as the central atom. 

🤜 The element with the lower electronegativity is generally the central atom.

🎗It is important to consider the following facts for molecules and ions with one central atom. 

(i) Identification of the central atom and surrounding atoms.

(ii) Calculating the total number of electrons for a given chemical formula considering all electrons in the valence shell of each atom.

👉👉e.g.: In H2O, oxygen atom contributes 6 electrons and one electron from each hydrogen atom (two electrons from two hydrogen atoms), which sum up to 8 when considering the total electron count (6 + 2 = 8) of the valence shells. 

👉👉If it is a negatively charged ion, then negative charges should be counted as well. e.g.: In the OH-ion, contribution of electrons from oxygen atom is six and hydrogen atom one together with one electron due to negative charge of the ion adding up to eight as the total number of electrons (6 + 1 + 1 = 8).

👉👉If the ion is positively charged, then an equivalent number is deducted from the total valance electron count.

e.g.: In NH4

+ ion, N atom contributes 5 valance electrons and four hydrogen atoms contribute 4 electrons. However, since it is a cation, then one electron (equivalent to number of positive charges) is deducted resulting 8 electrons in the valance shell of nitrogen atom (5 + 4 – 1 = 8).

(iii) A bond is denoted by a pair of dots between the central atom and a surrounding atom. Each surrounding atom is connected to the central atom with at least one bond.

(iv) Bonding electron pairs are denoted first as a pair of dots (Lewis dot diagram) or a short line (Lewis dot-dash diagram) drawn between central atom and each of surrounding atoms. Next, the remaining electrons are distributed, starting from the most electronegative atom, to complete the octet. Each electron pair is marked by pair of dots (lone pair electrons). If the electronegative atoms are surrounding atom, then lone pairs are marked on these surrounding atoms in order to complete the octet of each atom. CCl4 is an example for this.

In the case of ammonia, surrounding atoms are hydrogen, remaining pair of electrons is marked on the nitrogen atom.

In the Lewis dot diagrams bond electrons between two atoms can be represented as follows.

(v) If electron pairs are remaining after distributing electron pairs on the surrounding atoms (satisfying the octet rule), then left over pairs of electrons are marked on the central atom.

(vi) After distributing all the electron pairs, the number of electrons on each atoms should be compared with the number of electrons in the non-bonded state of the atom (free atom) to assign the formal charge and then check completion of the octet. In the case of a bond, one electron is counted for each atom and if lone pairs are present, both electrons are counted to the particular atom. Priority is given for completion of the octet.

As an example, NH2−ion:

Here the total electron count on the nitrogen atom is 8. Though the nitrogen atom has contributed only 5 electrons, from the Lewis dot diagram, it appears as if the nitrogen has contributed 6 electrons. Since it has one extra electron, (-1) the charge is marked on the nitrogen atom as the formal charge.

(vii) Electron distribution shall be rearranged in order to minimize the formal chargeon atoms and completion of octet by converting lone pair of electrons to bonding pairs of electrons.

If SO32−ion is taken as an example, sulphur atom will contribute 6 electrons and each oxygen will contribute 6 electrons. Hence 18 electrons come from three oxygen atoms. Addition of two more electrons due to (-2) charge add up to 26 electrons (6 + 3(6) + 2 = 26) for the Lewis dot structure.

All atoms of Lewis dot structure (d) have satisfied the octet, but it is not stable, since it has maximum formal charge distribution. Hence the lone pair electrons are rearranged in order to obtain the stable Lewis structure having minimum formal charge distribution. The following sketch shows the way of rearrangement.

Finally, the Lewis dot dash structure for SO32− is given as below.

Here, all oxygen atoms have completed octets. There are total of 10 electrons in the valance shell of sulphur atom which exceeds the octet. However, this is allowed due tothe presence of empty d orbitals in addition to the p orbitals in the valance shell of the sulphur atom.It is important to know the skeleton of atoms of a given chemical formula when multiple central atoms (e.g.: C3H6O) are present. Table 2.1 shows Lewis dot diagrams and Lewis dot-dash structures of selected molecules and ions.

Lewis dot diagrams and Lewis dot dash structures of some selected molecules and ions

You can also see

1.https://generalideasinchemistryforbegginners.blogspot.com/2021/01/just-introduction.html

2.https://generalideasinchemistryforbegginners.blogspot.com/2021/01/the-cathode-ray-experiment.html

3.https://generalideasinchemistryforbegginners.blogspot.com/2021/01/periodic-table-of-elements.html

4.https://generalideasinchemistryforbegginners.blogspot.com/2021/01/chemical-bonds.html

5.https://generalideasinchemistryforbegginners.blogspot.com/2021/01/covalent-bonds-and-dative-covalent-bonds.html

COVALENT BONDS And DATIVE COVALENT BONDS

 🎗Covalent bonds

Covalent bonds are formed when a pair of electrons is shared between two atoms of the same element or different elements. The sharing pair of electrons contribute one electronfrom each atom to form the electron pair. Consequently, stable electron configurationsare often achieved by both atoms in respect to the total number of electrons in the valence shells.Kossel, Langmuir and Lewis stated that the filling of electrons into a valance shell up to the maximum value of 8 results a stable electron configuration, hence called ‘octet’ rule.According to the current knowledge of electron configurations, the maximum number of valance electrons in 2s and 2p orbitals of elements in the second period (n=2) is 8.Therefore, elements in the second period complete the octet when forming chemical bonds thereby achieving a greater stability. This is more likely for elements such as C, N, O and F which form chemical bonds to complete the octet.

The valance shell of elements in the third period (n=3) and subsequent periods consist of d sub energy level in addition to s and p sub energy levels. Therefore, when forming chemical bonds, there could be instances where the number of electrons in the valance shell may exceed eight. Examples of such molecules are SO2 and SO3. In such molecules the number of electrons in the valance shell of sulphur is greater than eight. The presence of d orbitals in the valence shell of the sulphur atom permits 18 electrons. Since, the dorbitals in the valance shell also participate in bonding, the number of valance electrons in the sulphur atom can exceed the octet. However, for such atoms, it is not always necessary for the d orbitals to participate in bonding. For example, in the H2S molecule, the sulphur atom complete the octet without involving d orbitals.

There are other situations where atoms of some elements do not necessarily complete the octet. Elements like Be, B and Al form some electron deficient compounds such as BeCl2, BH3, BCl3 and AlCl3 are examples of such compounds with an incomplete valance shell. In the case of hydrogen atom where only 1s orbital is present, the stable electron configuration is achieved when the valance shell consists of two electrons. In all instances described above, the number of electrons in the valance shell after forming chemical bonds is an even number. However, this is not always true, as there are compounds such as NO and NO2 each having an odd number of electrons even without completing the octet.

🎗Dative covalent bonds 

In a molecule or ion, dative bonds are formed when atoms with empty orbitals interact with atoms with a lone pair of electrons. In certain cases when the free atom of the element 

has less than four valance electrons (as in Be, B), the number of covalent bonds that the particular atom can form is less than four. This results in incomplete octet with lower 

stability. Therefore, such electron deficient central atoms preferably react with the atom having lone pairs which can donate an electron pair to the central atom to complete the 

octet. The reaction of BH3 with CO to produce borane carbonyl and the reaction with CN- to produce cyanoborohydride are example with such dative bonds. Furthermore, reaction of NH3 with BF3 to form a dative covalent bond between B and N is another example. The dative bond is formed when the empty orbitals in B overlaps with the orbital having the lone pair in the nitrogen atom. In this case a central atom cannot be chosen precisely. 

Since the lone pair on the nitrogen atom is donating the electron pair to B, the bond can be denoted by an arrow. The arrow head is pointed to the electron deficient atom. This 

can be illustrated using formal charges as well as shown below.

Dative covalent bonds are also formed when metal ions or some metal atoms react with molecules or ions having lone pairs (H2O, NH3, CO molecules and CN-ions) in order to 

form complexes. The following illustrates the formation of a complex ion when Cu2+ is reacted with four NH3 molecules to form dative covalent bonds.

CHEMICAL BONDS

 Introduction 

Chemical bonds and structure of molecules are conceptual models based on the modern atomic model, in order to explain the physical and chemical properties of matter.Many atoms do not have stable outermost valance shell configurations, therefore chemical bonds occur between atoms in order to achieve stability. The following data explains how valence electrons participate in different types of chemical bonding using several acceptable models.

Chemical bonds

👉Sharing a pair of electrons between two atoms

1.Covalent bonds

Sharing a pair of electrons between two atoms in which each atom contributes one electron

2.Dative covalent bonds

Sharing of an electron pair between two atoms in which both electrons are given by one atom

👉Metallic bonds

Large numbers of metallic cations are stabilized by a cloud of many electrons

👉Co Complete removal of electrons from an atom to form cations and acceptance of electrons by another atom 

1.Ionic bonds/ Ionic interactions/ Ionic attraction forces

Formed due to electrostatic attractive forces between cations and anions

 

Periodic table of elements

 Introduction

 History of periodic table

The discovery of chemical elements has been ongoing since ancient times. Certain elements, such as gold (Au), appear in nature in elemental form and were thus discovered thousands of years ago. In contrast, some elements, such as technetium (Tc), are radioactive and intrinsically unstable and were discovered after the development of technology during the twentieth century.

As the number of known elements increased, scientists began classifying them. In 1869, Dmitri Ivanovich Mendeleev in Russia and Lothar Meyer in Germany published nearly identical classification schemes

Both noted that similar chemical and physical properties occur periodically when the elements are arranged in order of increasing atomic mass. Scientists at that time had noknowledge of atomic numbers.However with the introduction of the concept of atomic number the modern periodic table was

constructed.